Publication date: 2021-10-23
Update: 2021-12-08: minor grammatical corrections.
Update 2022-04-30: an even tinier edit.
A week or so ago my son asked me if I would help him with differential calculus when next he visits.
Of course! Really, dude, its pretty simple. A bit weird to get into, but once you've got the concepts sorted, its just like straight lines. We'll need to talk about the Limit Theorum, but from there, its pretty mechanical.
A few months previously we'd gone over the basics of straight lines and linear algebra because he was unhappy with his performance in his assessment. To the credit of the nation in which we reside they do oral assessments at high school. Not like the “sitting amongst a matrix of desks in silence" as I had experienced decades before. But, he got flummoxed in the moment, and more importantly with the tools he was being asked to use. He understood the problem, but was being prompted to use some computer program or whatever, when all he needed was a pencil and paper or a whiteboard.
In any case, we had fun sorting that one out, and he's unlikely to ever be "flummoxed" by simple linear equations again.
Lesson Planning
I did have a problem. How was I going to help with differential calculus? What was the "right" strategy? I settled on a similar method to that we'd used previously. I gave him some equations and tables for x and y with x filled in (-3, -2, -1, 0, ... 3). He was to fill in the y values from the equations. Then, he was to plot the graphs of the (x, y) values and we could talk about the graphical (geometric) representation of the numbers. Then, following that, we examined the algebraic side of the picture. A nice, calm, step-by-step, "shoot questions as we go" process. That seemed the right approach for this too.
But, Calculus is a pretty big thing, not for "difficulty" but "significance". So, there was going to be a need to mention Leibnitz and Newton and "Principia", and of course the Limit Theora which are the fundamental underpinning. That I could knock up in a few hours and had at least a week to prepare.
But, there was still a potential problem. I wanted to work with quadratic equations. He must have studied them by now if his teachers were throwing differential calculus at him!? He called yesterday, and yep, quadratics covered. Phew. Okay, so we've got quadratics, or more specifically non-linear (curved) continuous equations with which to work. This is a "Limit Theorum" thing. You need continuous non-linear equations (or functions, to be more precise) to get that working. If that makes no sense to you, don't worry, read on!
But, there was a deeper niggle. I have this habit of doing meditations on the structure of the universe, or more commonly the solar system, and sometimes the history of and prerequisites for science, and recently I've been meditating on the history of astronomy. There is a link hidden in here, and I wanted to use it in the teaching.
Parabolas
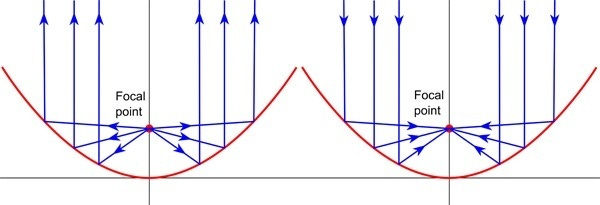
One of the strange and wonderous properties of the shapes that you get when you draw the graph of a quadratic equation, these shapes are called parabolas, is that they a have a focus. This focus is a single point near the base and on the line of symmetry for the parabola.
[Image: quora.com]
If you draw parallel lines coming "into" the parabola and "bounce" them off the point of contact, they all go to this focus, and vice versa. This rather special bidirectional property has applications in engineering whenever one wishes to direct or collect light. I haven't checked if this property was known before Newton (almost certainly) but Calculus must provide a way to demonstrate it.
Single direction incident “light” bounces off a whole curved surface precisely described by (differential) calculus and reflects to one exact place. Thus, the “calculus” must describe the one to one relationship between the “single direction” incident light and its “single” end point. There are no other variables.
My historical, astronomical meditation prompted me to make this the “voila!” of the session on calculus.
Galileo
I had recently watched a presentation by Jim Al-Khalili, a Syrian/British particle physicist/science communicator, in which he cited Galileo’s discovery using his newly built telescope, of the orbits of the four major moons of Jupiter. Being the first to see and thus "discover" the moons is big enough, but it was his extended observation of the moons that proved that they were orbiting Jupiter. These days we'd just say "of course, you dipstick" but back then European scientific inquiry was heavily influenced by the Roman Catholic Church and its doctrine was that: You are special, God loves you, the Earth is the center of the universe and everything in the Universe rotates around Earth. Galileo threw a few spanners into that dogmatic work when he published his little book describing what he'd seen with his telescope.
Understandably, Galileo was excommunicated from the Church. The point that Professor Al-Khalili was making, with which I heartily agree, is that this was one of the key moments in European science. It created the space to question dogma and propose heretical ideas, especially if you have the data! Science is sort of born out of the event. At least, it is an event that gives increased legitimacy to the proposal of new, possibly heretical, ideas backed by observed data, and the methodology used to perform the observation. Galileo doesn’t get all the “props”. Tycho Brahae, Copernicus and Kepler had big hands to play in the geo-centric to helio-centric shift, and Brahae gets the props for the data observation. I have visited the museum which preserves the site of his 16th century observations.
Newton, Again
However, there were a few shortcomings to Galileo's telescope. A key one was that its two lenses caused a blurring around the outer edges of the image. This is where Newton comes back into the (clearer) picture. His publication of Opticks in 1704, in English no less, revolutionized the way that the behaviour of light is understood. It took a little while longer to receive the work of the towering Scottish physicist James Clerk Maxwell's work on light as an electro-magnetic phenomena; the first major contribution in a long, still unfulfilled struggle towards unifying the fundamental forces of nature. Post Opticks, Newton redesigns the telescope. Instead of two lenses, there are no lenses (which produced the blurriness) but two mirrors. All optical or radio based "telescopes" from this point up until now have used this design. If there were patents in 1700 our celestial knowledge would be dark. Alternatively, the column inch length and frequency of publication of Astrology in any nation’s national “newspapers” is inversely proportional to the quality of its science education (™).
Recall that focus of the parabola. The "base" mirror of an optical telescope is a parabolic mirror. When observing distant objects one can assume that the incoming light is parallel and thus all of that light will be reflected towards the focus. If its a radio telescope, that's where you put the detector. If its optical, that's where you put a second mirror to send the light "sideways" out of the telescope for viewing.
So, this was my "cool idea". Quadratic equations, parabolas, Newton, and astronomy, with a bit of "Principia" here and "Limit Theora" there to create a nice teaching package. Its all rather easy if you're only teaching high school level maths/physics/history. So, I went to bed with the ideas not entirely formed but knowing that it felt good and that I had time to "iron out the details". But, as I lay there, happy and tired, I kept seeing a parabola with parallel incident light reflecting to the focus. I could not see the geometric mathematical certainty of the focus. I mean this quite literally. My brain was projecting images of 2-D space incident, parallel light onto a parabolic 2-D curve and drawing the lines to the focus, but they were not clear. I could not “feel” them. They were not “true”. But, I KNEW they had to be.
This is mathematical “cognitive dissonance”
This is a strange, and probably obsessive-compulsive or I-dont-know-what thing, but brains are what they are and mine would not let go. I awoke maybe 5 hours later before the sun had arisen and my brain said "No!" you shall not go back to sleep, you do not know this! It gnawed and excited.
So, partially annoyed, but really very enthused, coffee was made and work began. Normal people would just look stuff up on the internet and no doubt find some well produced and clear explanation/demonstration of whatever was to be conveyed. My feeling was that if I could not prove this to myself then I had no right to teach it to my son.
That "self proof" needed to be from first principles. No damn internet. I KNEW it had to be demonstrable, and I KNEW that all I needed was high school mathematics, physics and the formula for derivatives of quadratics.
I pay homage to the many great teachers that have helped me and that I have known and worked with. The way that I pay homage is that I prove to myself that I have learned the core of their syllabus, and honor them by teaching content that I can explain from first principles.
Showing pictures of my diagrams and writing proves nothing. I could have found these stupid ideas and created a deception. It is the horrific nature of the work that proves its origin. No self respecting mathematics graduate would ever admit to this rubbish.
A Viscous Dawn
By the time this page is finished, the sky out of my eastern window is blooming with reflected light off the morning clouds. The coffee is two thirds finished and stone cold.
And, there is an error in this. I had chosen to work on the (1, 1) point of the y = x^2 (x^2 is silly speak for “x squared”) graph, which was a very bad choice. The graph shows the key insight I needed in that cluttered space of the diagram with “180 - 2θ” this and “90 - θ” that. Around this center point are these talisman Thetas (θ: Greek letter often used in mathematics for angles). In the lower left two "Thetas" contain the key. I am working with the tangent to the parabolic curve, which is the line with the two thetas either side. There is also a vertical line. We know from Cartesian geometry that the opposite angles of two intersecting straight lines are the same. (Calm down, its only a bit longer). Thus, the lower and upper angles are θ (the same). The insight is the lower left θ. The vertical line is "bouncing" off the tangent line, and Newton's Opticks tells us that the angles coming in and going out from a reflection are identical. A little Greek symmetry, a little English alchemy and a crowd of thetas to give us the two equations uniting the unknown.
All the other scribbles are just my hand deliberately slowing my brain down so it doesn't get too excited.
On the right side you can see an arrow pointing to h = 1/(4/3) which is h = 3/4.
This is the magic number. I then proceed to clarify/verify/re-express. Happily, I quickly recognize that "something is wrong". This is where (1, 1) comes in. (Top right corner, in the red box in the first “working” image). NEVER work with a point like that. (2,4) or (3,9) would have saved me a little time, but also prevented me learning a little more for myself. Why never? Dont ask. 1’s just come up all over the place in maths and you have to keep an eye on whether they relate to the geometry or the algebra.
Ok. The diagram is good at its core. It just needs to be abstracted. Get rid of (1, 1). It needs to be "pure" maths. Another page or two of doing that and verifying my numbers:
Now it is time. The mathematics is horrible, but it is consistent. I check the web. Yep, one quarter is the y coordinate at the origin for the y = x^2 parabola, and my "equation" produces it for points at x = 1, 2 and 3. "Type it up".
Lets be clear here. I have an equation for pumping in 3 numbers which all produce the same output. I am certain that an elegant proof disentangles the "tan" and "artan" and just disappears the x and y because they are not needed; its a bloody constant. The “steepness” of the graph “f’(x)” needs to be used, but x and y are truly irrelevant.
This clumsy method demonstrates another point in science. Verify your work. This is horrible mathematics, but bearable engineering. No elegance, but verifiable, consistent results. I am both embarrassed and proud.
The Joy of Learning
What does the teacher want?
The simple answer to this unasked question is, joy. For a teacher the great joy is experiencing a determined student break through confusion into curiosity, with energy!
Time to brush up on Limit Thera …
PS: For you science nerds out there, you should have noticed the N/A in the final image. My son will get this exact question because it is important to understand what mathematics does and cannot.
Annex
Years earlier when my son was learning about triangles and trigonometry we played a "game". For a triangle there are 6 fundamental quantities which define it. The lengths of the three sides and the quantity of the 3 internal angles. I claimed that if one knew three of these things, and at least one of them was a side length, then all others and the area of the triangle could be derived. Purists would rightly declare that this is only true for "flat" triangles.
So, we set ourselves a puzzle. A triangle was drawn and one side length and two angles labelled. The puzzle was, work out the other 4 quantities.
I recall that we hit a block. We both got "stumped" at one point. But, it was a game and so we just took a break. On return it was the younger partner who spotted the way through the blockage. Power on from there we did, and all quantities were calculated.
It may have been this game of playing with a triangle that lead to the more structured work on linear equations, and will lead to the upcoming structured work on calculus. My little "proof to myself" of the focus involved two equations from two triangles.
They remind me to integrate play into our learning calculus.
Sources
Jim Al-Khalili, his site
Opticks, Sir Principia, Wikipedia
Parabola, Wikipedia
(Should be Sir) James Clerk Maxwell, Britannica
Galileo Galilei, Stanford Encyclopedia of Philosophy, 2021
Hey, Vel.
Do Not Subscribe: This blog does not and will not ever issue "notifications". Do not "subscribe", it wont help. Use RSS. The URL is the obvious: https://yesxorno.substack.com/feed .
If you like what you read here then thank the author by sharing it.
Copyright and Licensing
This work is copyright to the blog's author with CC BY-SA 4.0 licensing. Have fun, reuse, remix etc. but give credit and place no further restrictions. Lets build culture. https://creativecommons.org/licenses/by-sa/4.0/legalcode